
(1) American mathematician Claude Elwood Shannon was born in Gaylord, Michigan on April 30, 1916. Shannon's father was a judge in a small town of Gaylord, and his mother Mabel was the principal of the local high school. When a child, Shannon turned out to be mathematically precocious and got a taste of science from his grandfather, who was an inventor and a farmer and whose inventions included the washing machine and farming machinery.

(2) From an early age, Shannon showed an affinity for both engineering and mathematics, and graduated from Michigan University with degrees in both disciplines. For his advanced degrees, he chose to attend the Massachusetts Institute of Technology. At the time, MIT was one of the prestigious institutions conducting research that would eventually formulate the basis for what is now known as the information sciences. Its faculty included mathematician Norbert Wiener, who would later coin the term cybernetics to describe the work in information theories that he, Shannon, and other leading American mathematicians were conducting. It also included Vannevar Bush, MIT's dean of engineering, who in the early 1930s had built an analog computer called the Differential Analyzer which was developed to calculate complex equations. It was a mechanical computer, using a series of gears and shafts. Its only electrical parts were the motors used to drive the gears. This work formed the basis for Shannon's influential 1938 paper "A Symbolic Analysis of Relay and Switching Circuits," in which he put forth his developing theories on the relationship of symbolic logic to relay circuits.
(3) Shannon graduated from MIT in 1940 with both a Master's degree and Doctorate in mathematics. After graduation, he spent a year as a National Research Fellow at the Institute for Advanced Study at Princeton University. In 1941, Shannon joined the Bell Telephone Laboratories, where he became a member of a group of scientists charged with the tasks of developing more efficient information transmitting methods and improving the reliability of long-distance telephone and telegraph lines. While working at the Bell Labs they started to develop the theory of the error-correcting code.
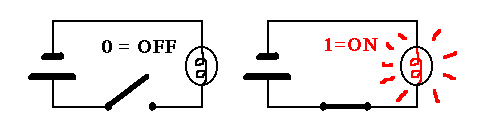
(4) One of the most important features of Shannon's theory was the concept of information entropy1случайность, беспорядочность (как явление в физике). Entropy happened to be equivalent to a shortage in the information content in a message and this fact was proved by Shannon. According to physics' second law of thermodynamics, entropy is the degree of randomness2энтропия, сбой в любой системе, возникающий с определенной периодичностью in any system which increases over a period of time. Thus, many sentences can be significantly shortened without losing their meaning. Moreover a signal proved to be sent without distortion. So this concept has been developed over the decades into sophisticated error-correcting codes that ensure the integrity of the data on which society interacts. While studying the relay switches on the Differential Analyzer, Shannon noted that the switches were always either open or closed, or on and off. This led him to think about a mathematical way to describe the open and closed states. Shannon theorized that according to a binary system a switch in the on position would equate to one and in the off position, it would be a zero. Reducing information to a series of ones and zeros, he noticed that it could be processed by using on-off switches .He believed that information was no different than any other quantity and therefore could be manipulated by a machine.
(5) Shannon's most important scientific contribution was his work on communication. In 1941 he began a serious study of communication problems, partly motivated by the demands of the war effort. This research resulted in the classic paper entitled "A mathematical theory of communication" in 1948. This paper founded the subject of information theory and he proposed a linear schematic model of a communications system. Communication was then thought of as requiring electromagnetic waves to be sent down a wire. The idea that one could transmit pictures, words, sounds etc. by sending a stream of 1s and 0s down a wire, something which today seems so obvious was fundamentally new. It was in this work that Shannon first introduced the word 'bit,' comprised of the first two and the last letter of 'binary digit' to describe the yes-no decision that lay at the core of his theories.
(6) Combining mathematical theories with engineering principles he set the stage for the development of the digital computer and the modern digital communication revolution. The results were so breathtakingly original, that it took some time for the mathematical and engineering community to realize their significance. But soon his ideas were picked up, elaborated upon, extended, and complemented with new related ideas. As a result a brand-new science had been created in the form of Information theory, with the publication of that single paper, and the frame work and terminology he established remains standard even today.

(7) During the World War II, Alan Turing, a leading British mathematician spent a few months working with Shannon. Both scientists were interested in the possibility of building a machine that could imitate the human brain. In the 1950s, Shannon continued his efforts to develop what was then called "intelligent machines" - mechanisms that emulated the operations of the human mind to solve problems.
(8) Shannon's information theories saw application in a number of disciplines in which a language is a factor, including linguistics, phonetics, psychology and cryptography. His theories also became a cornerstone of the developing field of artificial intelligence, and his famous conference at Dartmouth College in 1956 was the first major effort in organizing artificial intelligence research. He wrote a paper entitled "Programming a computer for playing chess" in 1950, and developed a chess playing computer. Shannon's interest did not stop with these. He was known to be an expert juggler who was often seen juggling three balls while riding a unicycle. He was an accomplished clarinet player, too.
(9) "Shannon was the person who saw that the binary digit was the fundamental element in all of communication," said Robert Gallagher, a professor of electrical engineering who worked with Shannon at the Massachusetts Institute of Technology. "That was really his discovery, and from it the whole communications revolution has sprung," considered Marvin Minsky of M.I.T., who as a young theorist worked closely with Shannon.
(10) Shannon received a plenty of numerous honorary degrees and awards. His published and unpublished documents (a total of 127) cover an unbelievably wide spectrum of areas. Many of them have been a priceless source of research ideas for others. One could say that there would be no Internet without Shannon's theory of information; every modem, every compressed file, every error correcting code owes something to Shannon.
(11) Shannon died at age 84 on February 27, 2001 in Medford, Mass., after a long fight with Alzheimer's disease.
Adapted from the Internet sites
